INSTRUCTION CACHE COMPRESSION
ABSTRACT
Code compression could lead to less overall system die area and therefore less cost. This is significant in the embedded system field where cost is very sensitive. In most of the recent approaches for code compression, only instruction ROM is compressed. Decompression is done between the cache and memory, and instruction cache is kept uncompressed. Additional saving could be achieved if the decompression unit is moved to between CPU and cache, and keeps the instruction cache compressed as well. In this paper, we explored the issues for compressing the instruction cache. In the process, we discuss a high level implementation for a 64-bit, 5-stage pipeline MIPS like processor with compressed instruction cache. The discussion is carried with the help of a compression algorithm with instruction level random access within the compressed file. In addition we present a branch compensation cache, a small cache mechanism to alleviate the unique branching penalties that branch prediction cannot reduce.
Code compression is a general technique. The most commonly used algorithms for block compression are variations of Huffman and arithmetic that compresses serially within the block, byte wise. A feature of Huffman coding is how the variable length codes can be packed together. A more sophisticated version of the Huffman approach is called arithmetic encoding. In this scheme, sequences of characters are represented by individual codes, according to their probability of occurrence. This has the advantage of better data compression, say 5-10%. Run-length encoding followed by either Huffman or arithmetic encoding is also a common strategy.
In this paper we modify the Code Compressed RISC Processor (CCRP) algorithm to compress the instruction cache. The original CCRP algorithm faces the problem of additional stages of DEC and CLB for single 64-bit instruction and granularity of random access. The modified algorithm can solve the above two problems. But branch penalty is another problem encountered by the modified algorithm. In order to avoid this, we suggest a method called Branch Compensation Cache.
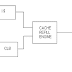
Figure-1: COMPRESSED CODE RISC PROCESSOR (CCRP)
It breaks the program into blocks of n, where n corresponds to the cache line size. Each block is compressed individually by a suitable algorithm. A Line Address Table (LAT) is used to record the address of each compressed cache line within the compressed program. Cache Lookaside Buffer (CLB) is added to alleviate LAT lookup cost. During program execution, upon each cache miss, LAT entry cached in CLB is used to calculate the compressed cache line address. The compressed cache line is then fetched from memory, decompressed, and placed into the instruction cache.
The details of rest of the paper is as follows:
- necessary modifications for the processor
- compression algorithm
- branch compensation cache
MODIFICATION OF THE PROCESSOR :We consider a 64-bit simple scalar instruction set, which is similar to MIPS We assume a simple 5-stage pipeline processor for ease of discussion. In order to compress the instruction cache, decompression must be done after the cache. Therefore the CPU must now be modified to include 2 additional functions.
Ø Address translation from the uncompressed version to the compressed (CLB)
Ø Instruction Decompression. (DEC)
These 2 additional sections are added to the usual 5-stage pipeline as shown in figure 2.
The CLB section implements address translation from the uncompressed version to the compressed version for each instruction and DEC implements Instruction Decompression.
The Instruction Fetch (IF) stage will now fetch the compressed instruction instead of the uncompressed instruction. The stage length for CLB and DEC are both dependent on the compression algorithm.
The additional CLB and DEC sections are both before the Instruction Decode (ID) stage. Thus stages within these sections will add to branch penalty. In addition, these penalties cannot be reduced by branch prediction since they are before the ID stage, where instruction opcode is first being identified.
Modified Algorithm: We devise such an algorithm. It can be thought of as a binary Huffman with only two compressed symbol lengths, but due to its similarity to table lookup we refer to it as Table. It uses 4 tables, each with 256, 16-bit entries. Each 64-bit instruction is compressed individually as follow:
i. Divide the 64-bit instruction into 4 sections of 16-bit.
ii. Search content of table 1 for section 1 of the instruction. If found, record the entry number.
iii. Repeat Step (ii) for section 2 with table 2 and so on with remaining sections.
iv. If entry number in the corresponding table replaces all the sections, then the instruction is compressed. Otherwise, the instruction remains uncompressed.
v. A 96-bit LAT entry tracks every 64 instructions. 32-bits equals the compressed address. The rest of 64 bits are on or off depending on whether the corresponding instruction is compressed or not.
Since this method tracts each instruction individually, the inter-block jump problem is gone. For the DEC section, decompression is either nothing or 4 table lookups in parallel. So one stage is sufficient. For the CLB section, it is simply a CLB lookup follow by some adding in a tree of adders. This could be done in one cycle, with CLB lookup taking half and adding taking another half.
Result for the Modified Algorithm:
Figure 3 is the compression result for Table compression. On average Table can compress to 70% of the original size. In comparison to CCRP with Huffman byte serial compression at block size of 8, we loose about 20% on average. This 20% lost is partly due to the smaller granularity of random access we have achieved. In general the smaller granularity of random access, the less compression will be achieved. This can be observed again with Gzip’s result, which does not provide any random access. On average it compresses to 20% of the original size, which is 30% better than CCRP with Huffman.
BRANCH COMPENSATION CACHE (BCC)
Problem: As mentioned earlier, in order to perform decompression after instruction cache (between the I-cache and the CPU), we add two more stages into the pipeline before ID: CLB (Cache Lookaside Buffer) and DEC (decompression). As a result, branch penalty is increased to three cycles. This is illustrated in figure 4.
Figure-5 USE BCC TO REDUCE BRANCH PENALTY
In figure 5, a PC jump is found at the ID stage, so we go to check BCC to see if the target instruction is pre-stored there. If no, then we have to go through CLB, DEC and ID pipeline stages; but if yes, then we simply fetch it and keep going, no branch penalty at all in such case.
Figure-6: BCC IMPLEMENTATION:
Figure 6 shows a more detailed pipeline implementation, where the key points are:
Ø At ID stage we find out a jump instruction being taken, so we must flush the current pipeline and restart.
Ø The restarted pipeline is used to get the target instruction through normal stages, i.e. using CLB to get the compressed address from the regular address, using IF to fetch the decompressed instruction, using DEC to decompress it to get target instruction. Simultaneously, we also go to the BCC to check if the required target instruction is pre-stored there. If no, then keep running the restarted pipeline; if yes, then we directly fetch the target instruction from BCC and flush/restart the pipeline for a 2nd time.
Ø The 2nd restarted pipeline is used to provide the sequential instructions after the jump. In order to completely eliminate the penalty incurred by a jump, we require T, T+8, T+16, T+24 instructions are all pre-stored in BCC upon a hit. So the 2nd restarted pipeline starts CLB stage with T+32 instruction, where T is the target instruction, T+8 is the next instruction, and so on.
Result: To quantify the BCC performance, we observed several applications such as ijpeg, wave5, etc
Figure-7: BCC PERFORMANCE
CONCLUSIONS:
We observe a tradeoff between granularity of random access and compression rate, where smaller granularity implies less compression. To avoid access branch penalty, smaller granularity of random access than CCRP is forced in order to compress the cache. Consequently, compression is less in instruction ROM than CCRP scenario. This drawback offsets any saving in instruction cache, except in region where instruction cache is big relative to overall system. Instruction cache compression is effective in embedded system, related to area where cache performance is more important than the instruction ROM die area. For example, in high performance computing, where large instruction cache is useful in improving hit rate, but painful in dealing with the critical path analysis. Here with instruction cache compression, one could potentially provide cache performance that is 1/ (compression rate-LAT) times the physical size.
REFERENCES
1. Wayne Wolf, Embedded RISC Architecture;
2. Barry.B.Brey, Introduction to Microprocessors;
3. Morris Mano, Computer Architecture & Organization;
4. Y. Yoshida & B.Y. Song, Code compression approach to Embedded Processors.





can iget help to make a report f 30 pages
ReplyDeleteshare it pc
ReplyDeleteMua vé máy bay tại Aivivu, tham khảo
ReplyDeletegia ve may bay di my
chuyến bay hồi hương từ mỹ về việt nam
khi nào có chuyến bay từ canada về việt nam
vé máy bay từ nhật bản về việt nam
Các chuyến bay từ Incheon về Hà Nội hôm nay
Vé máy bay từ Đài Loan về VN
vé máy bay vietjet từ nhật về việt nam